백준 Q1307 마방진
문제
https://www.acmicpc.net/problem/1307
마방진이란 NN의 격자의 각 칸에 1부터 NN까지의 정수를 정확히 하나씩 채웠을 때, 모든 가로줄, 세로줄, 대각선의 합이 같은 배치를 말한다.
예를 들면, 다음은 3*3 마방진 중 하나이다. 가로줄, 세로줄, 대각선의 합이 모두 15로 같다는 것을 알 수 있다.
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
N이 주어졌을 때 N*N 마방진을 구해보자
입력
첫째 줄에 자연수 N이 주어진다. (3 ≤ N ≤ 300)
출력
N*N 마방진을 아무거나 출력한다.
풀이
마방진을 만드는 규칙은 N이 홀수일때, 4로 나누어 떨어질 때, 그리고 4로 나누어 나머지가 2일때 각각 다르다. 입력은 3에서 300이라 위 3가지 규칙을 모두를 구현해야 한다. 먼저 홀수 마방진부터 본다.
홀수 마방진
아래 과정이 홀수 마방진을 만드는 과정이다.
- 시작은 첫 행, 한 가운데 열에 1을 둔다.
- 행을 감소, 열을 증가하면서 순차적으로 수를 넣어간다.
- 행은 감소하므로 첫 행보다 작아지는 경우에는 마지막 행으로 넘어간다.
- 열은 증가하므로 마지막 열보다 커지는 경우에는 첫 열로 넘어간다.
- 넣은 수가 n의 배수이면 행만 증가한다. 열은 변화없음.
위 방법으로 3,5,7,… 등 모든 홀수로 된 마방진을 만들 수 있다.
private static int[][] odd(int n, int[][] maBangJin){
// 1. 시작은 첫행 / 열은 한 가운데부터 시작
int r = 0;// 행
int c = n/2;// 열
int number = 1;
while(number <= n * n){
if(maBangJin[r][c] == 0){
maBangJin[r][c] = number;
number++;
}
//5. 넣은 수가 n의 배수이면 행만 증가한다. 열은 변화없음.
if(maBangJin[r][c] % n == 0){
r = (r + 1 + n) % n;
}
else{
//2. 행 감소 열을 증가 순차적으로 수를 넣어간다.
//3. 행이 첫 행보다 작아지는 경우에는 마지막 행으로
//4. 열이 마지막 열보다 커지는 경우에는 첫 열로
r = (r - 1 + n) % n;
c = (c + 1 + n) % n;
}
}
return maBangJin;
}
4N 마방진
짝수 중 4로 나누어 떨어지는 마방진을 만드는 과정이다.
- N * N 정사각형을 위의 도형대로 색으로 구분해준다.
- 좌측위부터 우측아래까지 가로로 1부터 N*N까지 채운다\
- 핑크색 부분은 그대로 두고, 파란색 부분은 NN의 중심과 대칭점인 부분과 숫자를 바꾼다.
(이렇게 생각하면 될 것이다. 원래 핑크색 기준 순서대로라면 I가 들어가 되는데, 파란색은 I가 아닌 NN + 1에서 I를 빼준 값을 넣어주면 N*N의 중점 중심으로 대칭이 된다.)
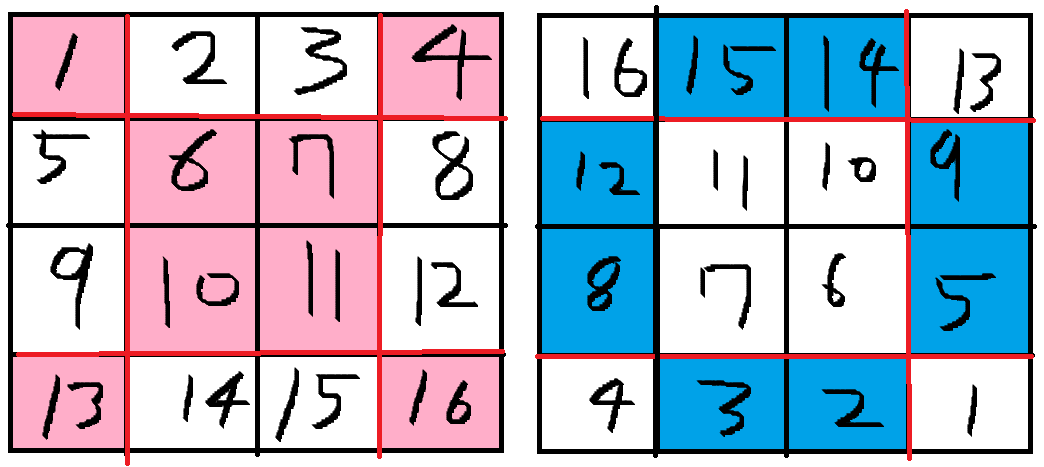
핑크색 부분과 파란색 부분을 나누어 생각하자면 위의 그림을 합친 그림으로 이해하면 된다. 핑크색은 좌측위부터 우측아래까지 좌측부터 1,2,3,4… 순서대로 먹인 것이고, 파랑색은 반대로 우측아래부터 좌측위까지 우측부터 순서대로 먹인 것이다. 위 둘을 색깔있는 것끼리 합치면 마방진 완성이다.
private static void even4n(int n, int[][] maBangJin){
int number = 1;
// 기본은 1부터 N*N까지 좌에서 우로 위에서 어래로 차례대로 숫자 넣기
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
// 만약 변경되어 있는 부분은 중점 기준 대칭이 되는 위치의 값으로 넣기
if(isChangeDivision(i,j,n)){
maBangJin[i][j] = n*n+1 - number;
}else{
maBangJin[i][j] = number;
}
number++;
}
}
}
private static boolean isChangeDivision(int i, int j, int n){
int nd = n/4;
// 변경 부분 - 상
if((i >=0 && i < nd) && (j >= nd && j < 3*nd)){
return true;
}
// 변경 부분 - 좌
else if((i >= nd && i < 3*nd) && (j >= 0 && j < nd)){
return true;
}
// 변경 부분 - 우
else if((i >= nd && i < 3*nd) && (j >= 3*nd && j < 4*nd)){
return true;
}
// 변경 부분 - 하
else if((i >= 3*nd && i < 4*nd) && (j >= nd && j < 3*nd)){
return true;
}
return false;
}
4N+2 마방진
이놈이 참… 애를 먹는 부분이다. 필자도 여기서 고민하다 https://destiny738.tistory.com/246?category=48883 에서 참고한 부분이다. 4N+2 마방진을 구성하는 방법은 다음과 같다.
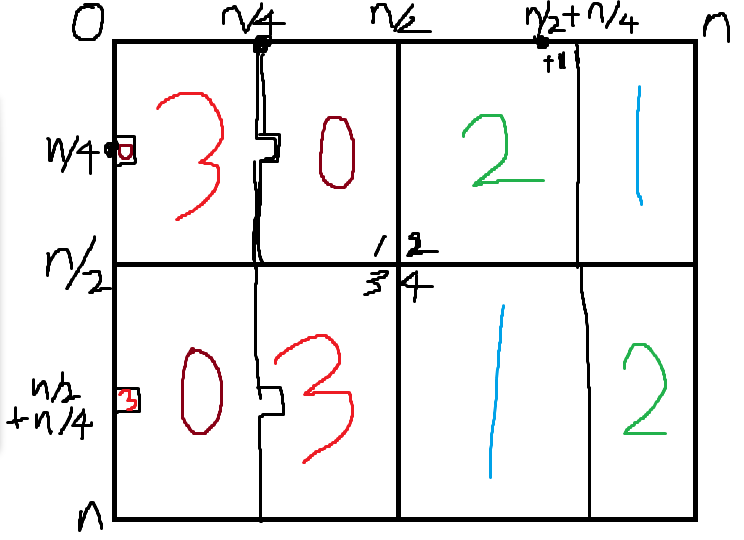
- N의 반절인 N/2의 마방진을 이전의 홀수 마방진 등록하는 방법을 이용하여 구한다.
- N * N 형태의 정사각형을 4개의 정사각형으로 4등분하여 위의 그림처럼 1,2,3,4 사분면으로 나눈다.
- 1사분면의 경우 0부터 N/4이전까지 열을 3으로 행으로 채운다. (단, n/4 행의 경우 첫 열은 0이고, n/4열은 3으로 채운다. 중앙이 뾰족 튀었다고 생각하면 된다.)
- 3사분면은 1사분면과 반대로 채운다.
- 2사분면은 N/2부터 N/4 + 1까지 열을 2로 행으로 채운다. 이후 나머지 열을 1로 행으로 채운다.
- 4사분면은 2분면과 반대로 채운다.
- 전체적으로 N*N/4를 곱해준다.
- 1번 과정에서 만든 홀수 마방진을 각 사분면에다 누적한다.
private static void even(int n, int[][] maBangJin){
int[][] oddMabangjin = odd(n/2, new int[n/2][n/2]);
// 1 사분면 - 3과 0 채우기
for(int i = 0; i < n / 2; i++) {
for(int j = 0; j < n / 2; j++) {
if(j < (n / 4)) {
maBangJin[i][j] = 3;
}
}
}
maBangJin[n / 4][0] = 0;
maBangJin[n / 4][n / 4] = 3;
// 3 사분면 => 1 사분면을 반대로
for(int i = n / 2; i < n; i++) {
for(int j = 0; j < n / 2; j++) {
if(maBangJin[i - n / 2][j] == 0) {
maBangJin[i][j] = 3;
}
}
}
// 2 사분면 2와 1 채우기
for(int i = 0; i < n / 2; i++) {
for(int j = n / 2; j < n; j++) {
maBangJin[i][j] = j <= n/2 + n/4 + 1 ? 2 : 1;
}
}
// 4 사분면 => 2 사분면을 반대로
for(int i = n / 2; i < n; i++) {
for(int j = n / 2; j < n; j++) {
maBangJin[i][j] = 3 - maBangJin[i - n / 2][j];
}
}
// 전체 n * n / 4 곱해주기
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
maBangJin[i][j] *= (n * n / 4);
}
}
// 홀수 마방진 누적하기
for(int i = 0; i < n/2; i++) {
for (int j = 0; j < n/2; j++) {
maBangJin[i][j] += oddMabangjin[i][j];
maBangJin[i][j + n/2] += oddMabangjin[i][j];
maBangJin[i + n/2][j] += oddMabangjin[i][j];
maBangJin[i + n/2][j + n/2] += oddMabangjin[i][j];
}
}
}
결론
이 문제는 마방진을 만드는 법을 아는가가 제일 큰 문제이다. 홀수 / 4N / 4N+2 형식의 마방진을 각자 만드는 3개의 문제가 종합적으로 돌어있는 문제로써 알아볼만 하다.
